First-Principles Investigation of the Interfacial Properties of Boron Nitride
Michigan Tech PhD. Defense
by Kevin Waters Follow along @ kwaters4.github.io/Presentation/Defense/
Hypothesis
Nanomaterials
Materials with at least one dimension in the sub-micron range.
- Ratio of surface to bulk atoms changes
- Bulk properties are not present at this scale
- Adding one atom changes the properties of the material
- Large configuration spaces to search
- Prediction can be utilized, but caution should be practiced
Examples of Nanomaterials
- Clusters
- Nanoparticles
- Fullerenes
- Nanotubes
- 2D-Materials

Boron Nitride Nanotubes
- Predicted in 1994
- Synthesized in 1995
- Typically considred a wide band gap semiconductor
- Parameters to consider
- Chirality (n,n), (n,0), (n,m)
- Diameter
- Layers
- Excellent chemical and thermal stability
Boron Nitride Nanotubes
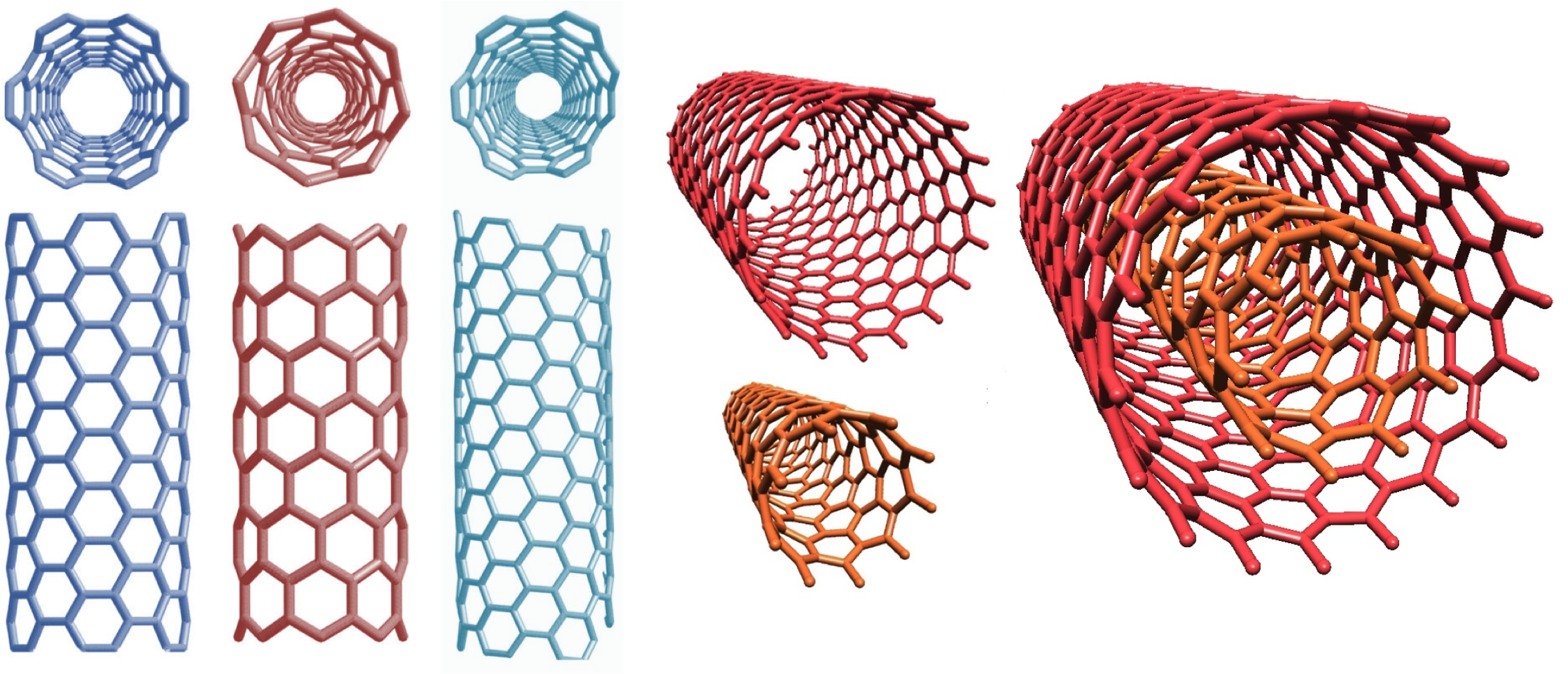
Difference between Carbon and Boron Nitride Nanomaterials
- Semi-ionic bonds (B-N) versus covalent (C-C)
- Interlayer interactions are stronger
- BNNTs are mostly zig-zag, CNTs statistcally equivalent.
- All BNNTs are semi-conducting, CNTs vary based on chirality
- Cytotoxicity still being investigated for BNNTs
Boron Nitride Nanotubes (Band Gap)
Biological Molecules
- Carbohydrates
- DNA (Nucleotides)
- Lipids
- Proteins (Amino Acids, Peptides)
- etc.
Methods and Tools
- Solving the system's electronic wavefunction
- Schrödinger Equation
- Density Functional Theory (DFT)
- Ab Initio Molecular Dynamics (AIMD)
- High Performance Computing Platform
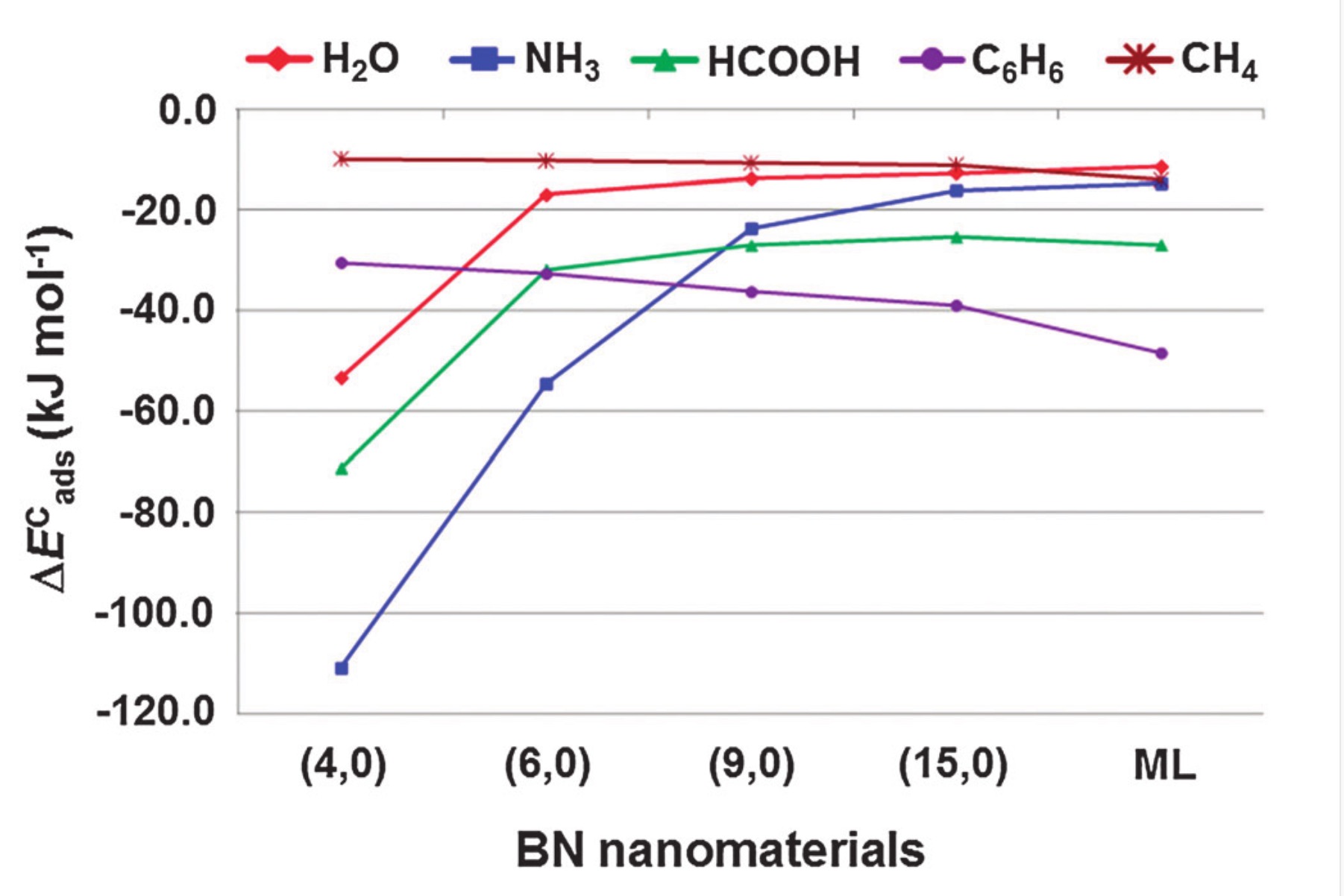
Amino Acids Adsorbed on Boron Nitride Nanomaterials
Proteins
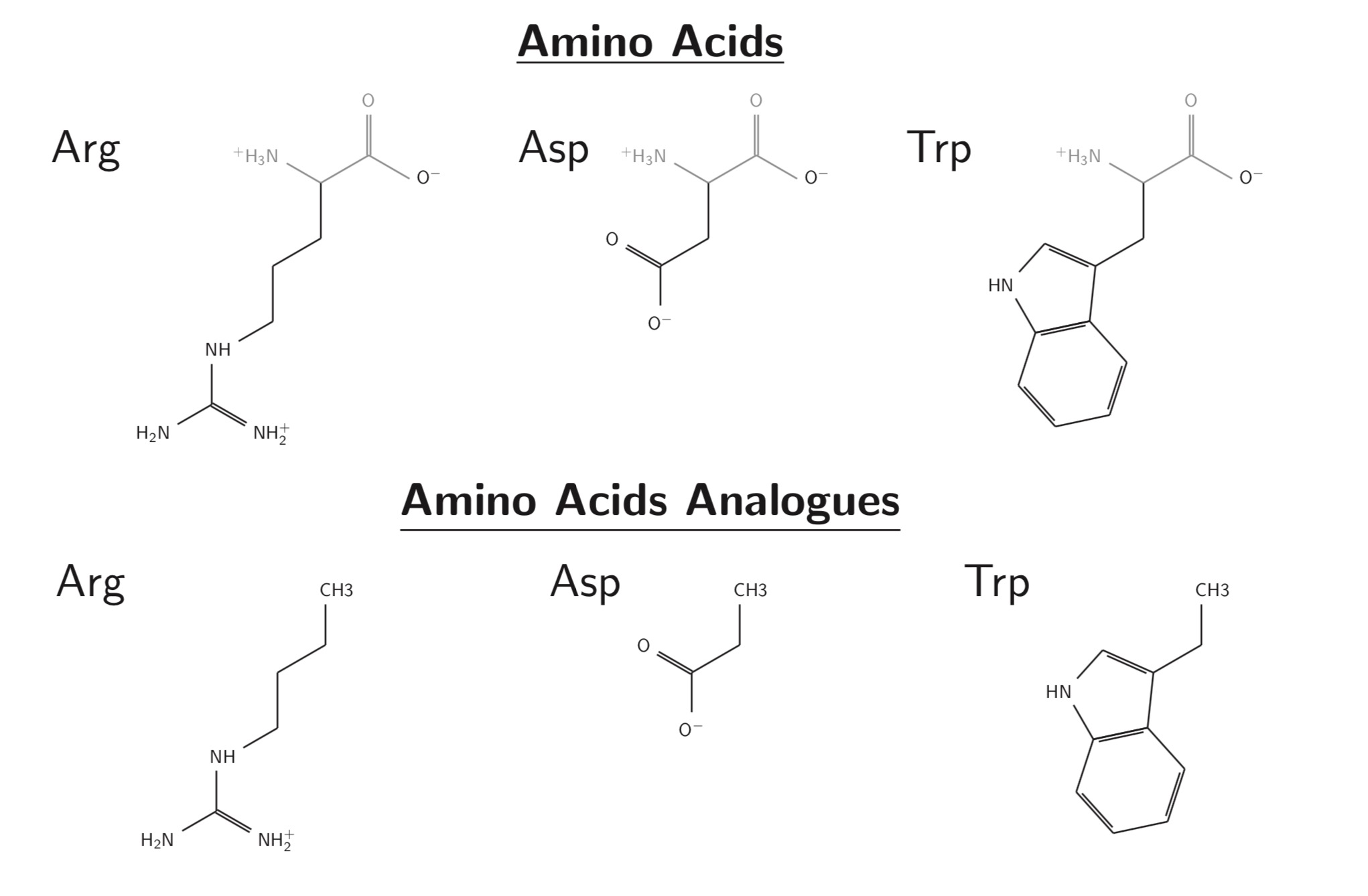
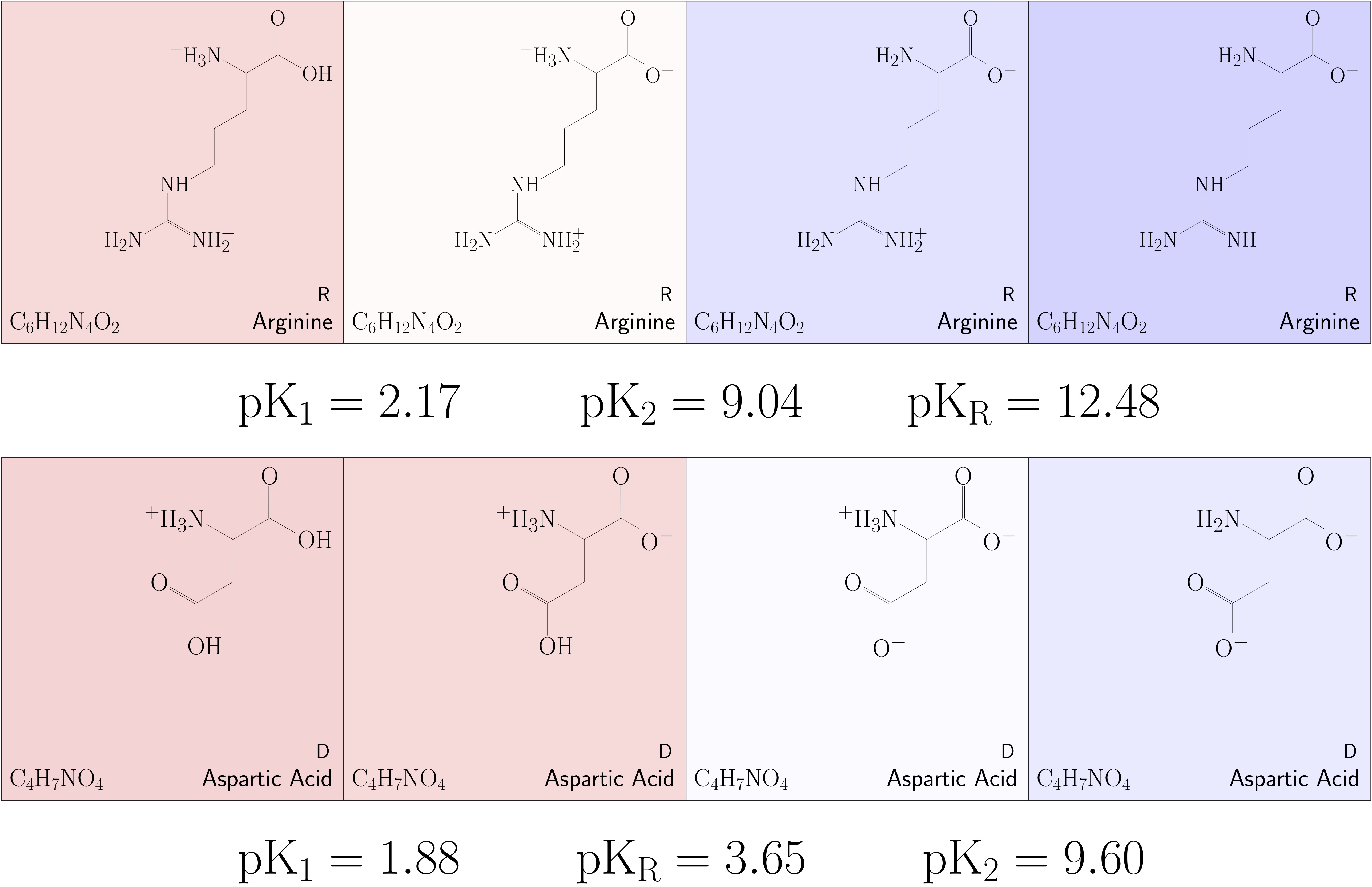
Adsorbed Structures
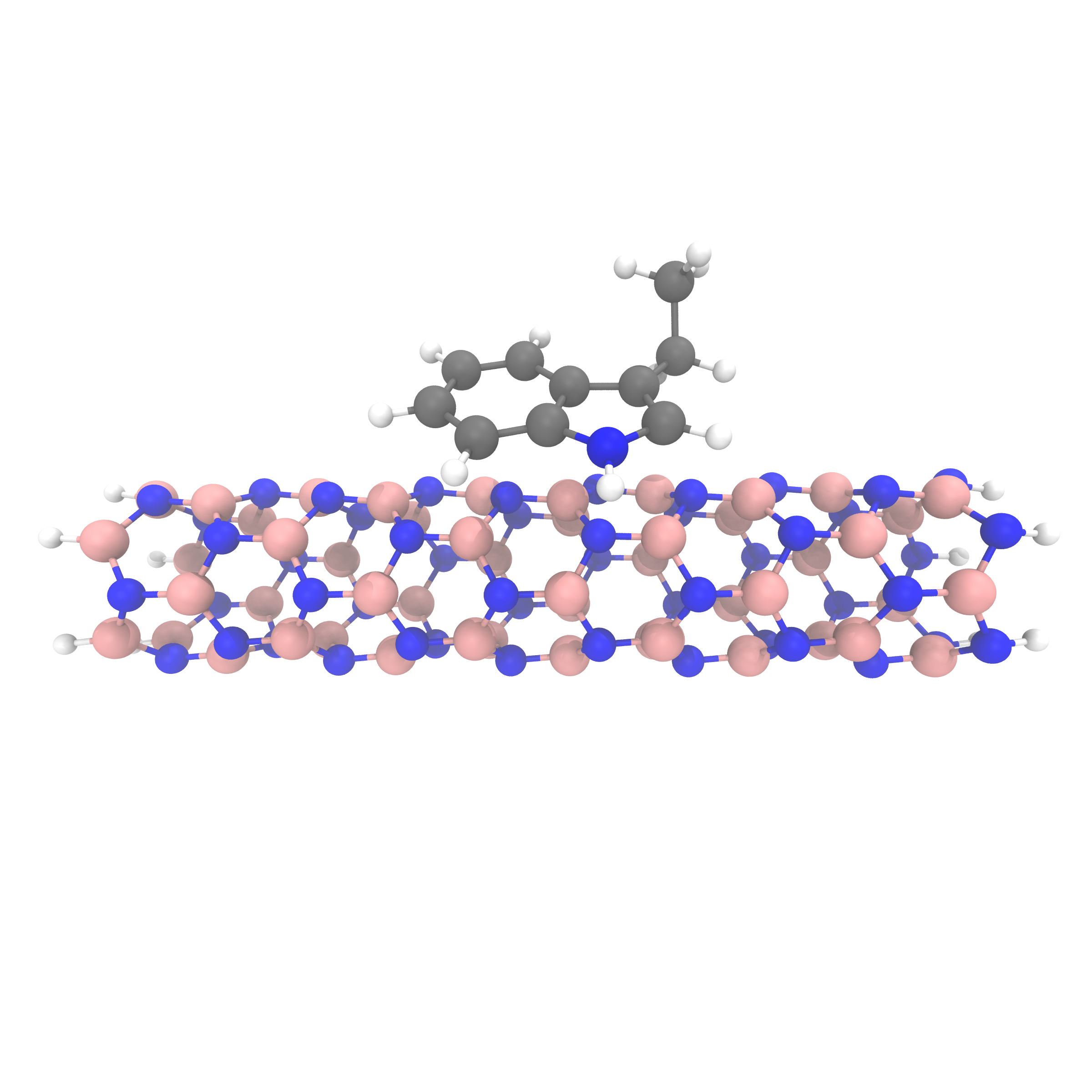
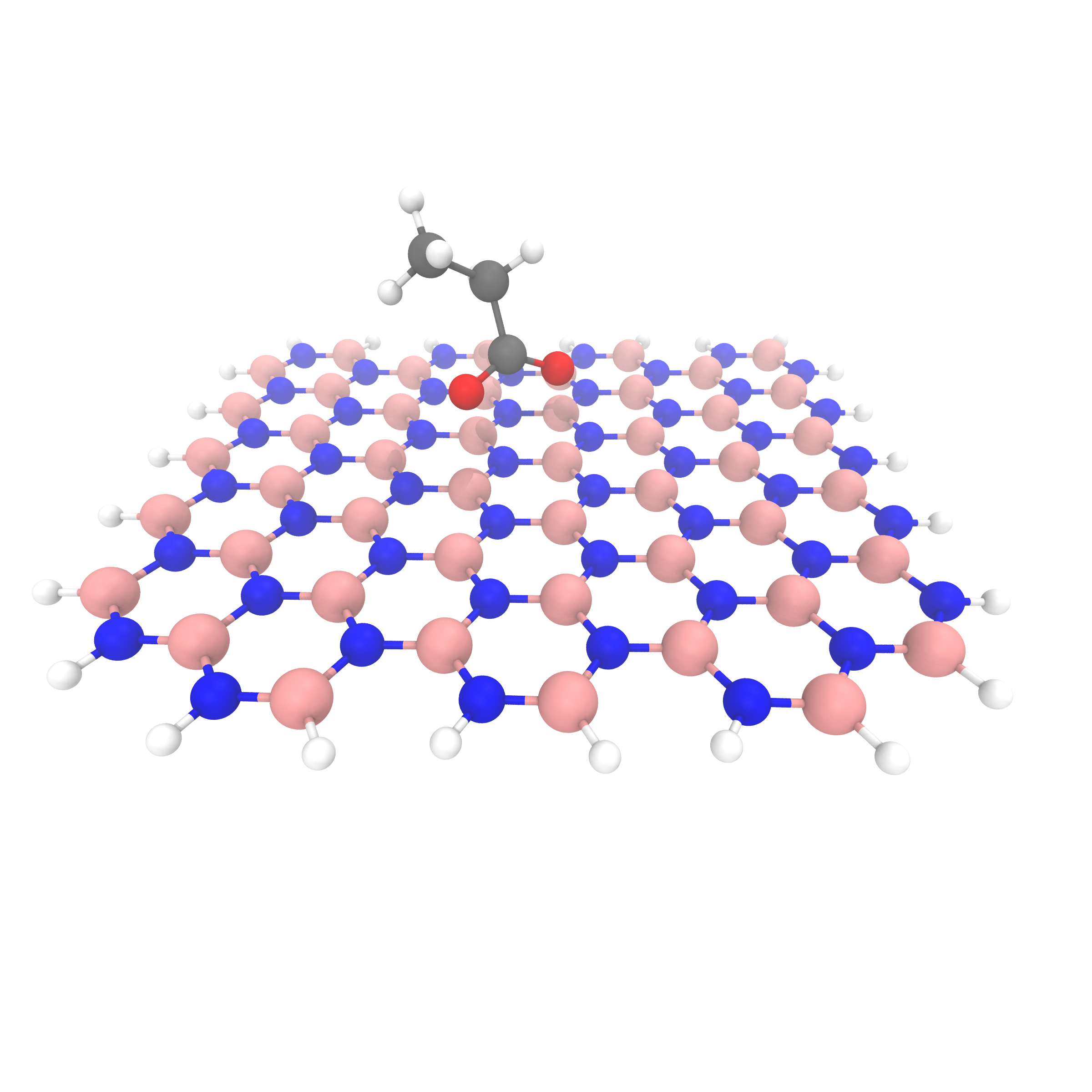
Binding Energies
Solvent effects on Boron Nitride using Ab Initio Molecular Dynamics (AIMD)
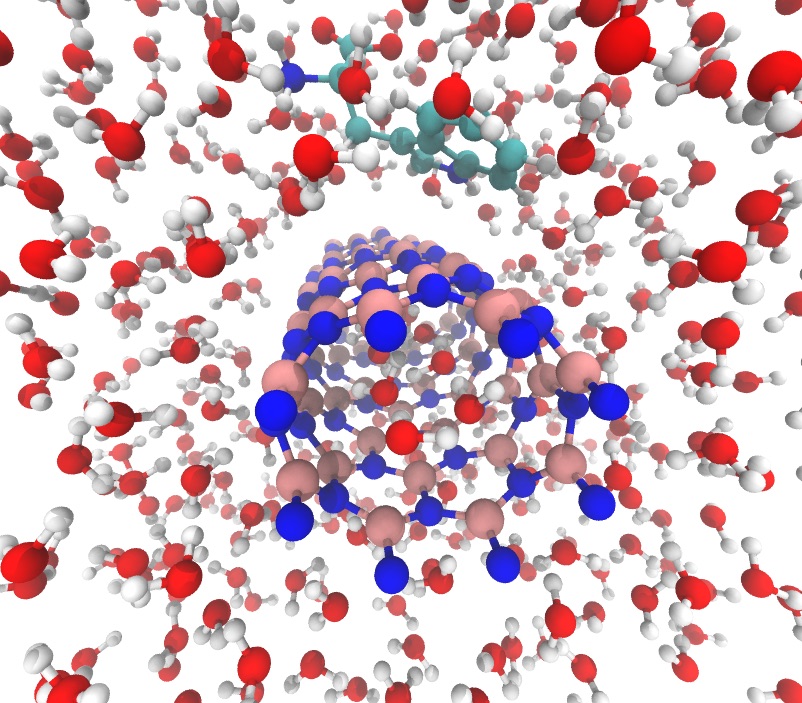
Structures of AIMD Simulations
Density Profile Calculation
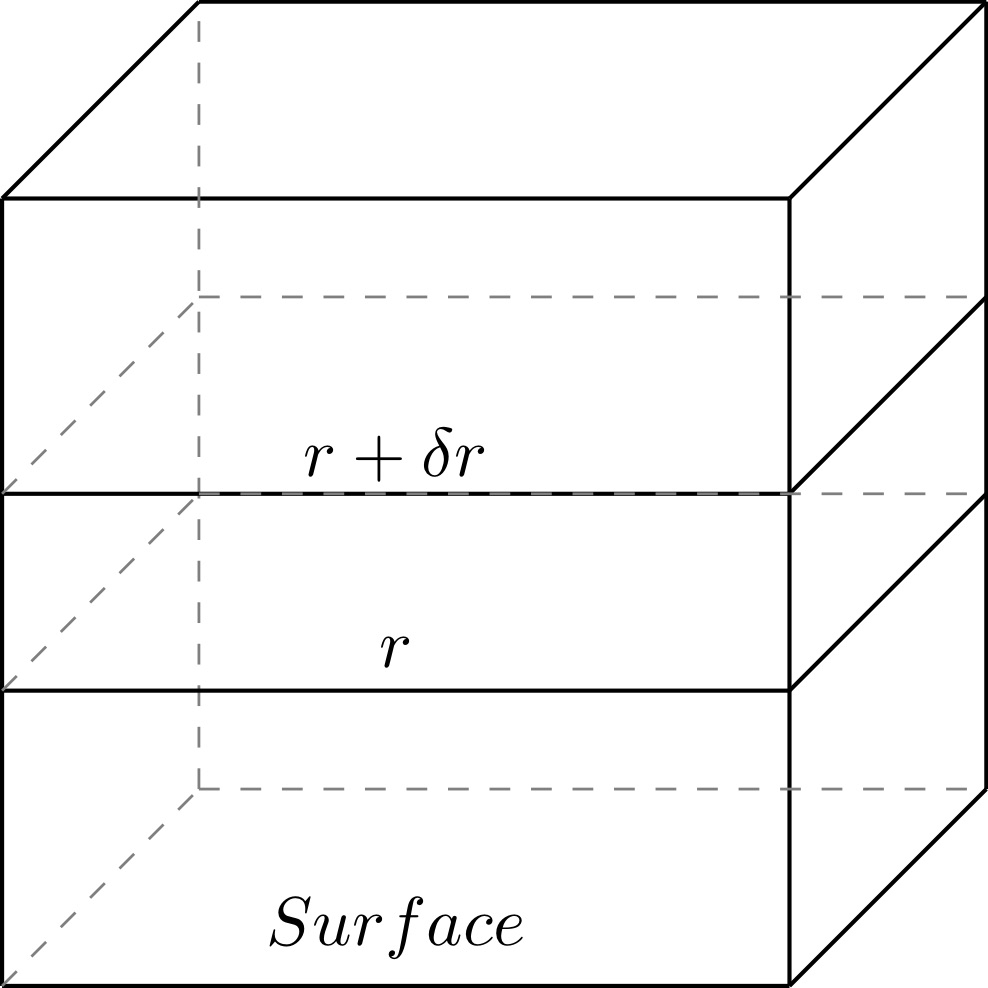 Monolayer
Monolayer
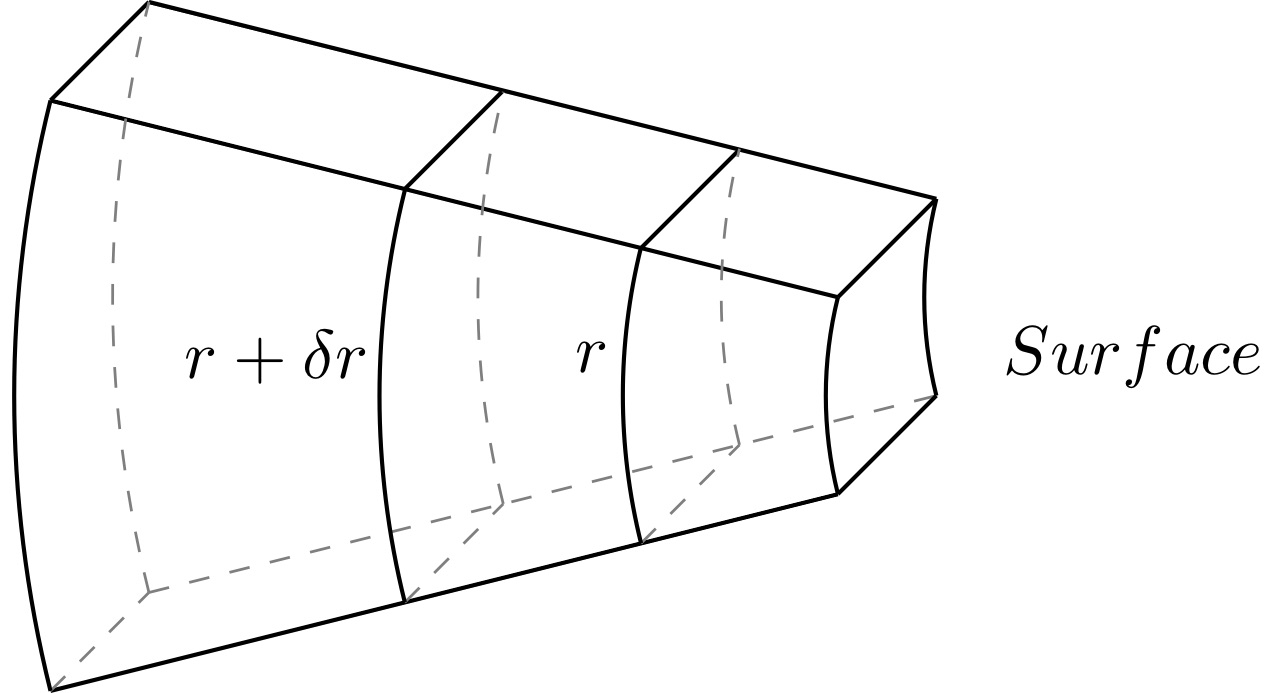
QM/MM Water Density Profile
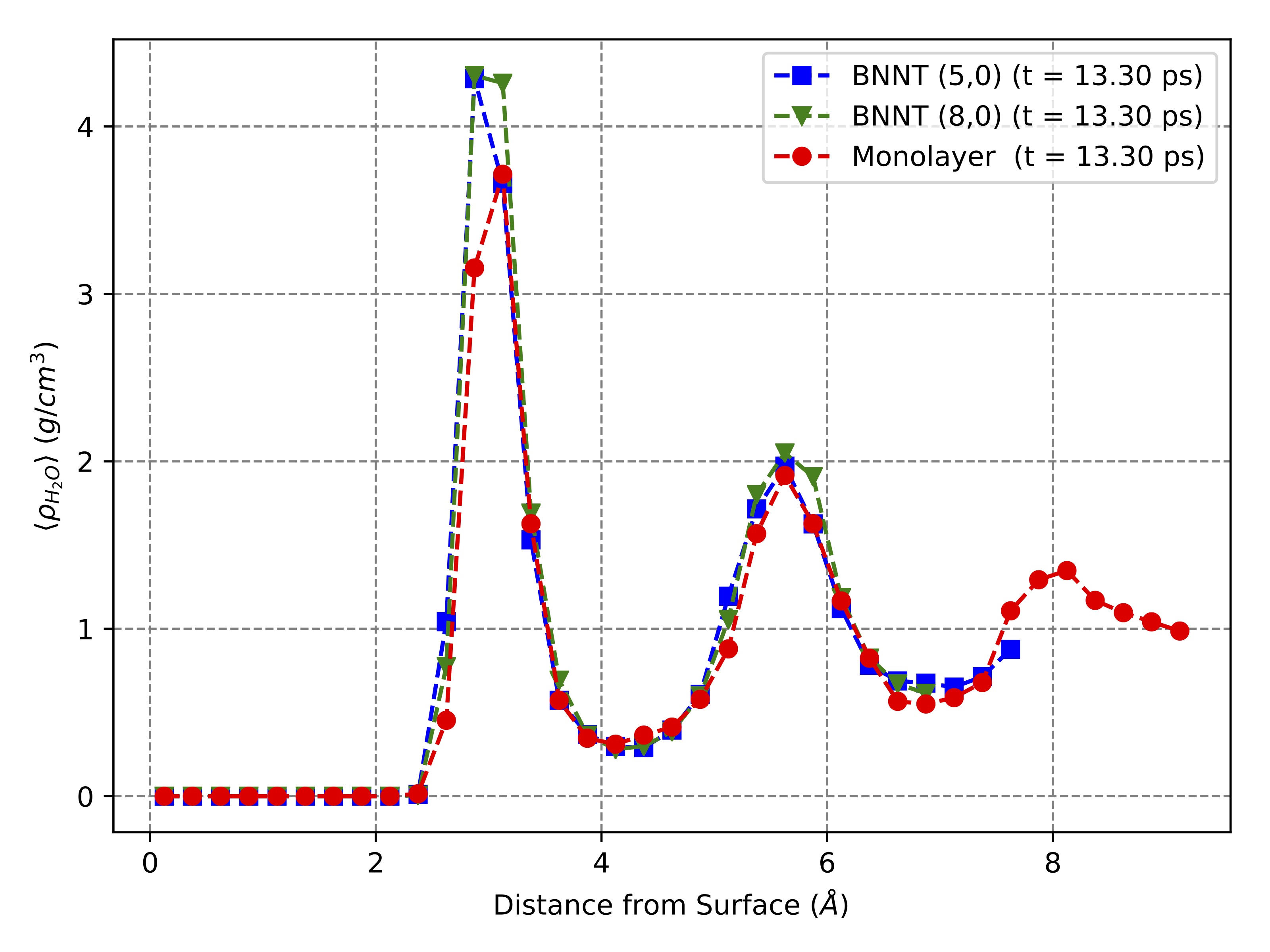
AIMD Water Density Profile
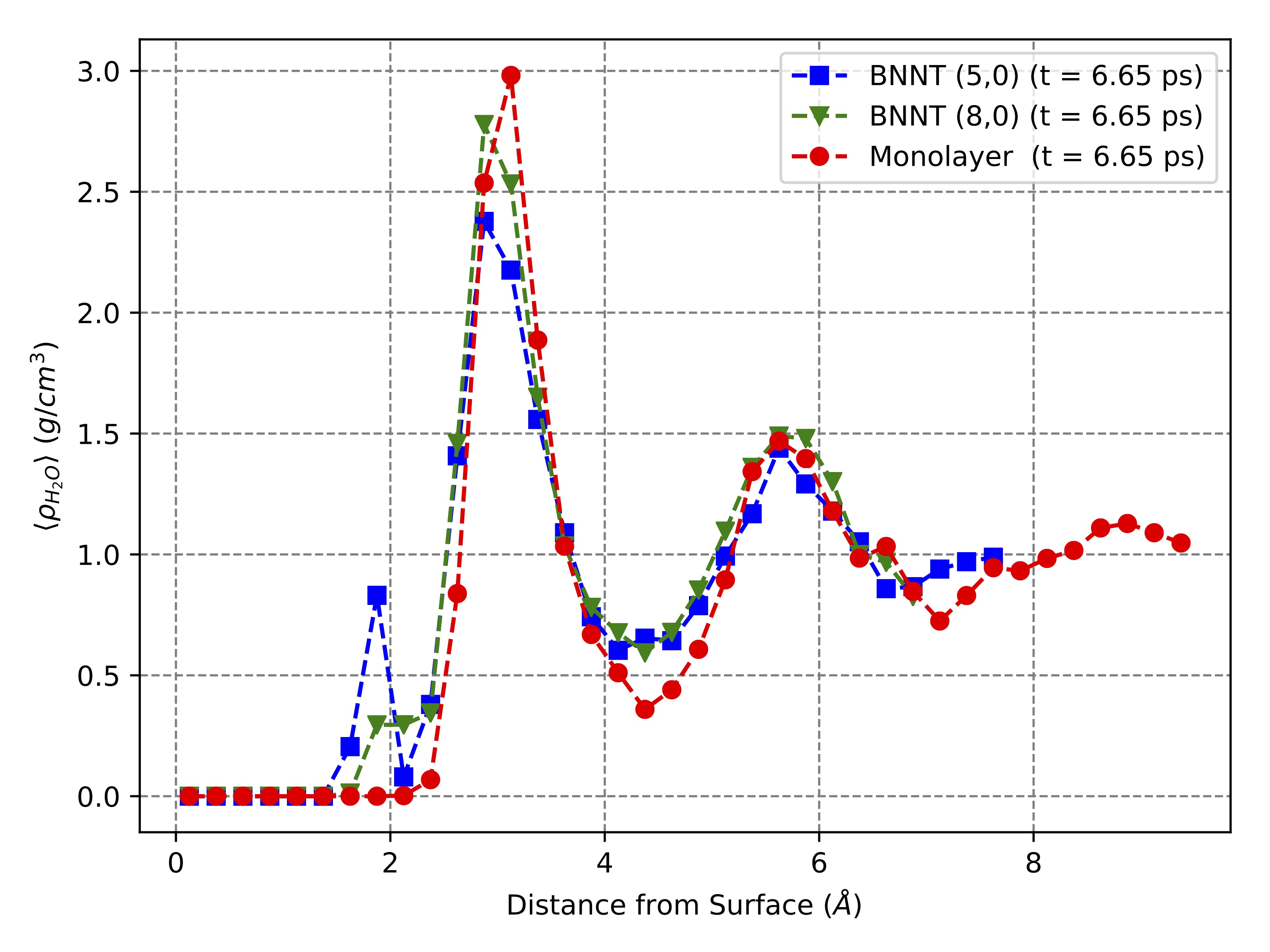
Future AIMD Work
- Continue using free-energy methods (PMFs & Metadynamics) to quantify amino acid binding energy
- Establish useful constraints for the free-energy methods
- Current limitation is computation time
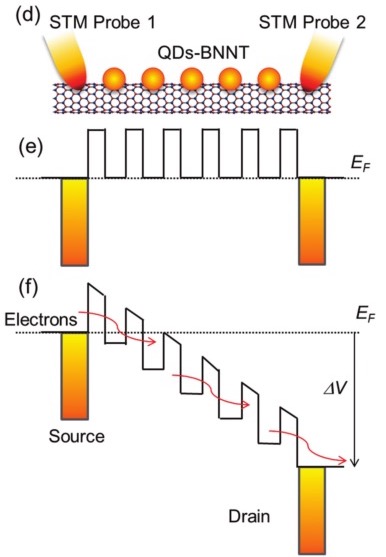
Gold Deposition on Boron Nitride Nanomaterials
Gold Quantum Dots on Boron Nitride

Boron Nitride Nanotubes Functionalized with Gold Quantum Dots
Gold Flakes on Boron Nitride
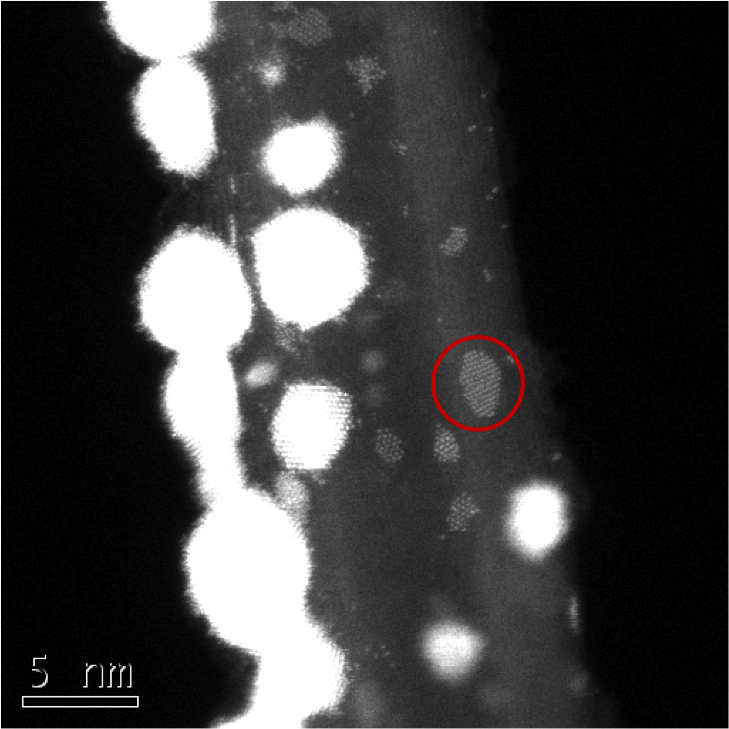
Unpublished work from Bhandari et. al.
Gold Flakes on Boron Nitride
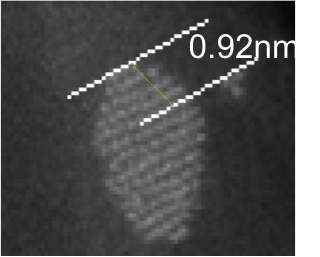
Unpublished work from Bhandari et. al.
Gold Cluster Structures
| 2D | 3D |
|---|---|
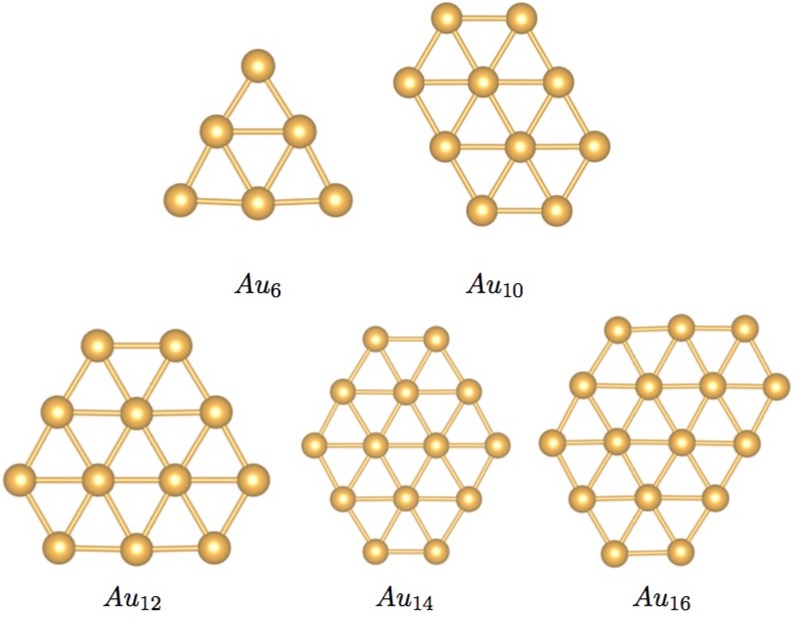 |
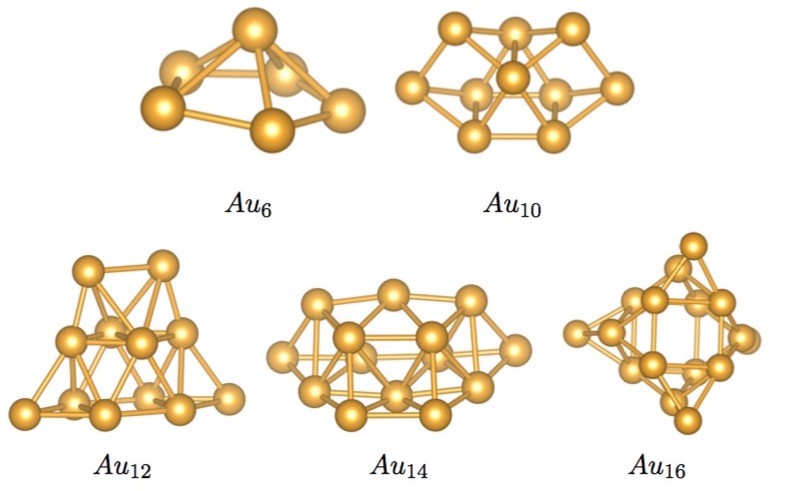 |
Gold Cluster Binding Energy
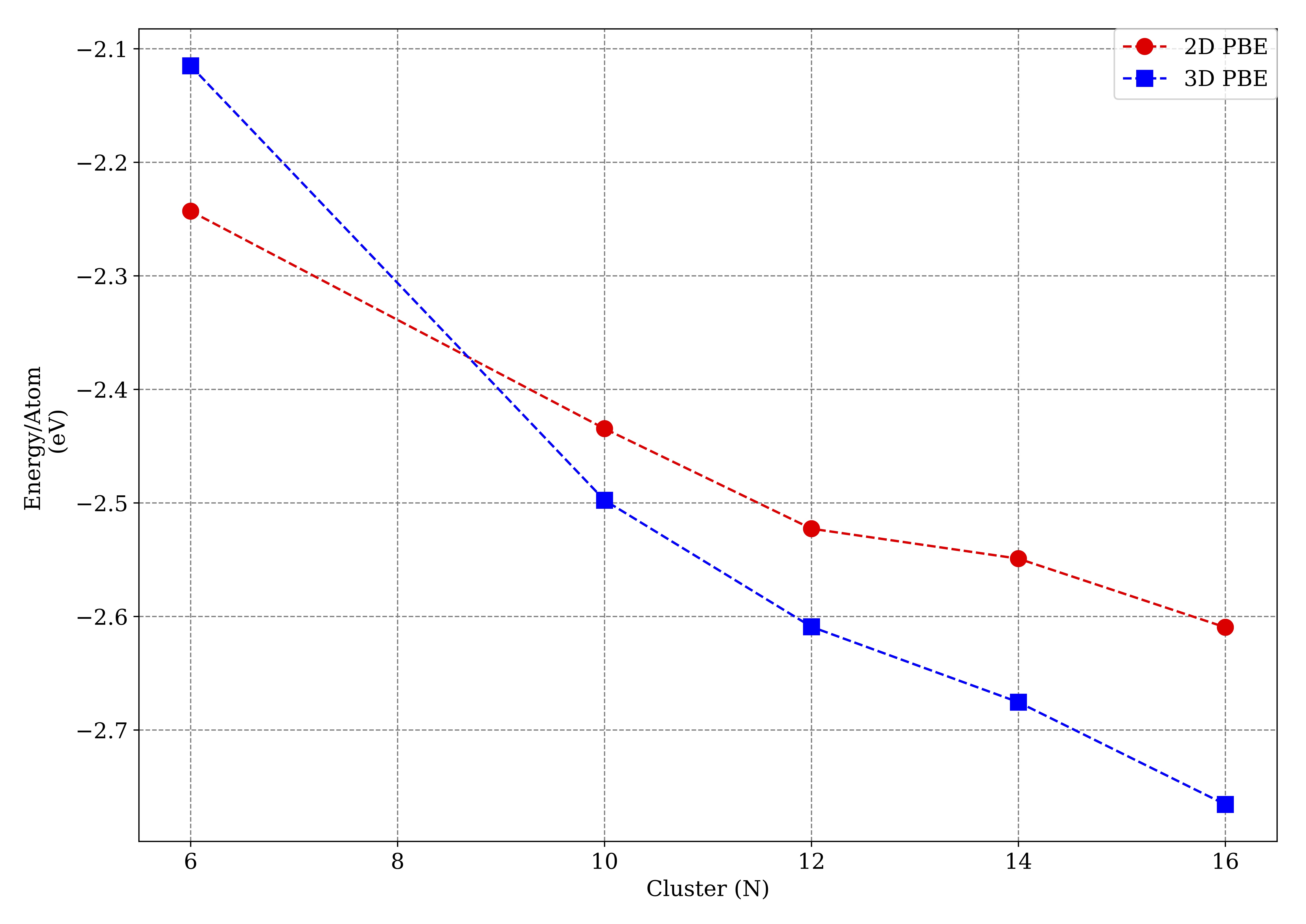
Gold Clusters on BN
Gold/BN Binding Energies
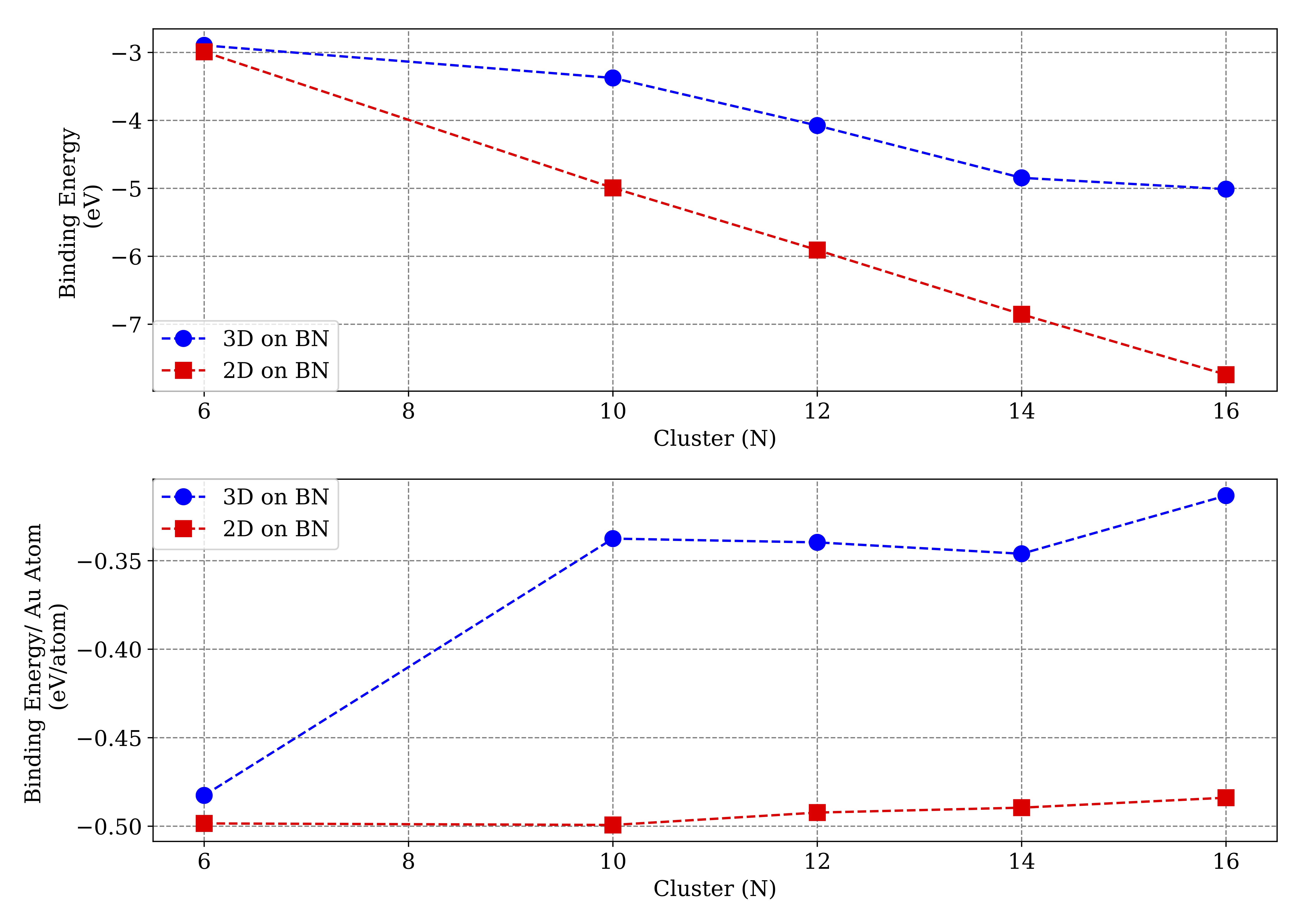
Gold Cluster Electronic Gap
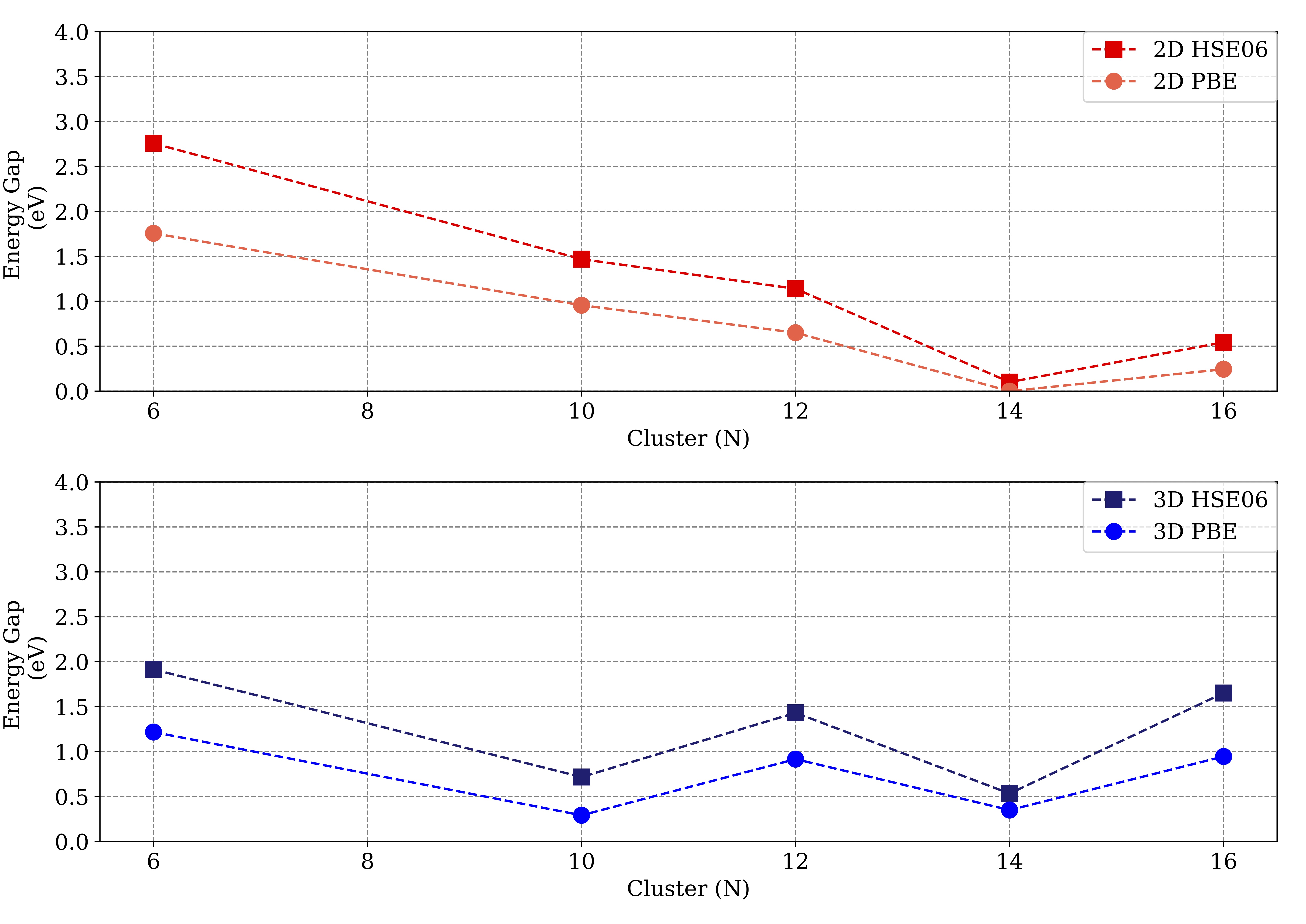
Conjugated Gold Cluster Electronic Gap
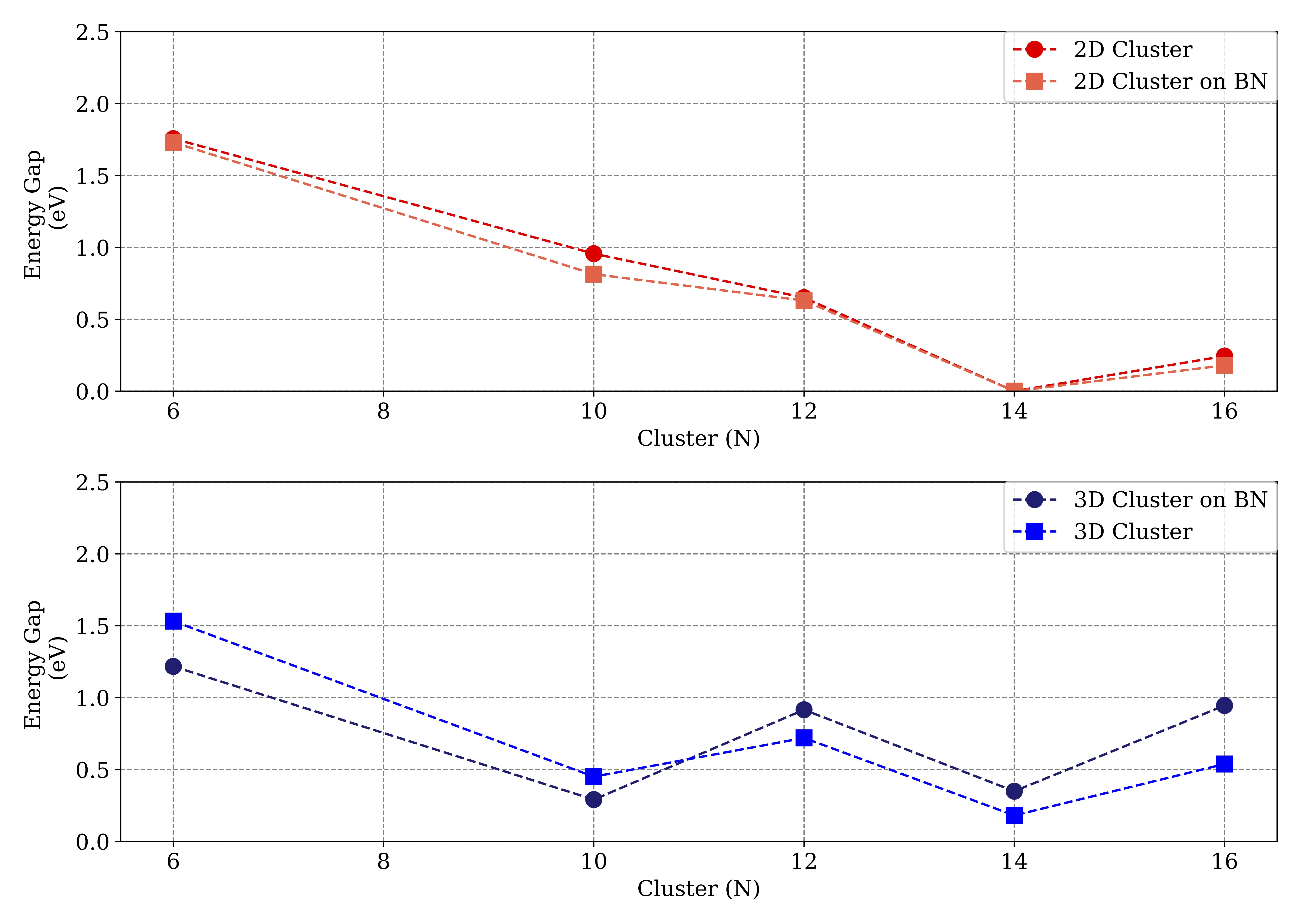
Mechanical Properties of 2D BN2
Experimental Functionalization
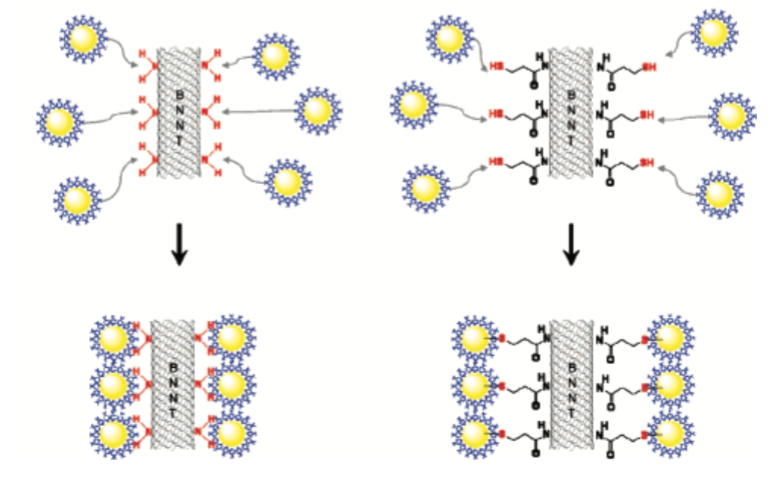
BN Electronic Structure Evolution
| Coverage (%) | Band Gap (eV) | Binding Energy (eV) |
|---|---|---|
| 0 | 4.25 | |
| 16 | 3.34 | -0.74 |
| 25 | 3.11 | -0.70 |
| 50 | 2.25 | 0.72 |

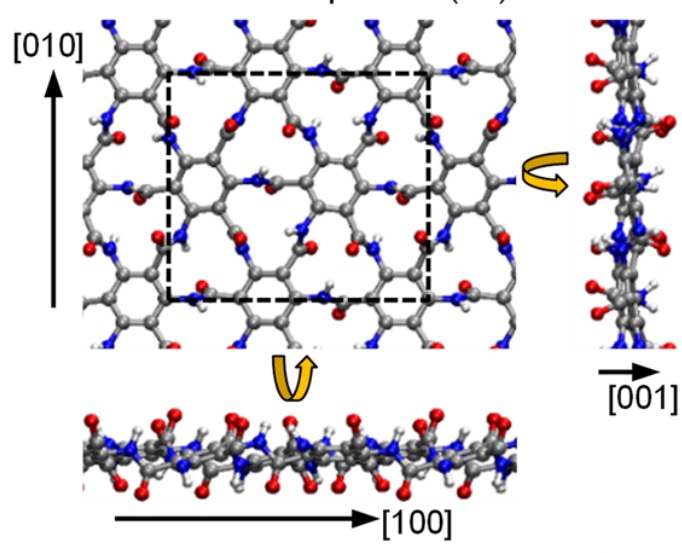
BN2 Monolayer
- Supercell : 2B + 4N
- Symmetry : Amm2 (38)
- Lattice Vectors
- a : 6.84 Å
- b : 2.55 Å
- Bonds
- N-N : 1.29 Å
- N-B : 1.34 Å
- B-N : 1.50 Å
- Stability : Phonon Spectra
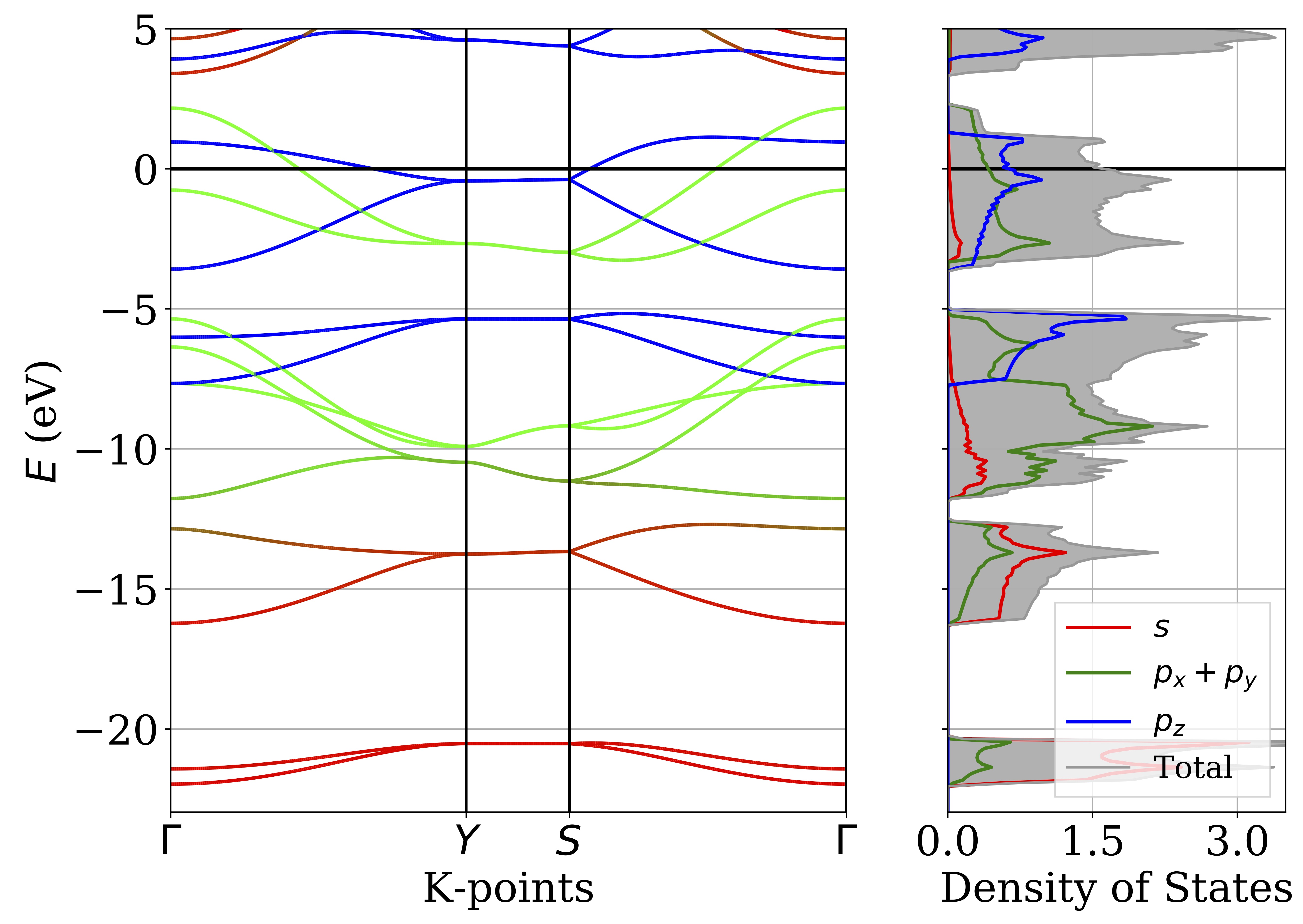
BN2 Band Structure (Orbital Projected)
Hooke's Law / Elastic Tensor
- σI is the stress tensor
- CIJ is the elastic tensor
- ηJ is the stain tensor
Orthorhombic Symmetry in 2D
Results
| N/m | Graphene1 | This Work | BN2 | This Work | |
|---|---|---|---|---|---|
| C11 | 358.1 | 353.7 | 293.2 | 290.5 | |
| C12 | 60.4 | 61.7 | 66.1 | 64.4 | |
| C22 | |||||
| C66 | 148.9 | 144.9 | 113.5 | 113.1 |
Results
| N/m | Graphene1 | BN2 | BN2 |
|---|---|---|---|
| C11 | 358.1 | 293.2 | 368.8 |
| C12 | 60.4 | 66.1 | 47.2 |
| C22 | 153.3 | ||
| C66 | 148.9 | 113.5 | 58.7 |
Exact-Exchange (Theory Development)
Formulation
Exact-Exchange in Real Space $$ \frac{1}{2} \sum_{\uparrow,\downarrow} \sum^{N^{\sigma}_{occ}}_{n=1} \sum^{N^{\sigma}_{occ}}_{m=1} \int\int_V \frac{\rho^{\sigma}_{nm}(\mathbf{r}) \rho^{\sigma}_{nm}(\mathbf{r})}{|\mathbf{r}-\mathbf{r'}|} d\mathbf{r} d\mathbf{r'} $$
Exact-Exchange in Reciprocal Space $$ \frac{1}{2\Omega} \sum_{\uparrow,\downarrow}\frac{1}{V_{BZ}^2}\int_{V_{BZ}} d\mathbf{k} \int_{V_{BZ}} d\mathbf{l} \sum^{N^{\sigma}_{occ}}_{n=1} \sum^{N^{\sigma}_{occ}}_{m=1} \sum_{\mathbf{G}} \frac{4\pi}{|\mathbf{G}-\mathbf{k}+\mathbf{l}|^2} \rho^{\sigma}_{m\mathbf{l};n\mathbf{k}}(-\mathbf{G})\rho^{\sigma}_{m\mathbf{k};n\mathbf{l}}(\mathbf{G}) $$
Filtered Potential $$ V_f{(\mathbf{G})} = \frac{1}{{V_{BZ}}^2} \int\int_{V} \frac{4\pi}{|\mathbf{G}-\mathbf{k}+\mathbf{l}|^2}d\mathbf{k}d\mathbf{l} $$
Seperation of Singularities (G=0)
$$ V_f{(\mathbf{G=0})} = \frac{1}{{V_{BZ}}^2} \int\int_{V_{BZ}} \frac{4\pi}{|\mathbf{l}-\mathbf{k}|^2}d\mathbf{k}d\mathbf{l} $$
$$ = \frac{4\pi}{{V_{BZ}}^2} \int\int_{V_{BZ}} \frac{1 - e^{\alpha|\mathbf{l} - \mathbf{k}|^2}}{|\mathbf{l}-\mathbf{k}|^2}d\mathbf{k}d\mathbf{l} + \int\int_{V_{BZ}} \frac{e^{\alpha|\mathbf{l} - \mathbf{k}|^2}}{|\mathbf{l}-\mathbf{k}|^2}d\mathbf{k}d\mathbf{l} $$
$$ \approx \frac{4\pi}{{V_{BZ}}^2} \int\int_{V_{BZ}} \frac{1 - e^{\alpha|\mathbf{l} - \mathbf{k}|^2}}{|\mathbf{l}-\mathbf{k}|^2}d\mathbf{k}d\mathbf{l} + \frac{8\pi^2}{V_{BZ}}\sqrt{\frac{\pi}{\alpha}} $$
Points with Singularities
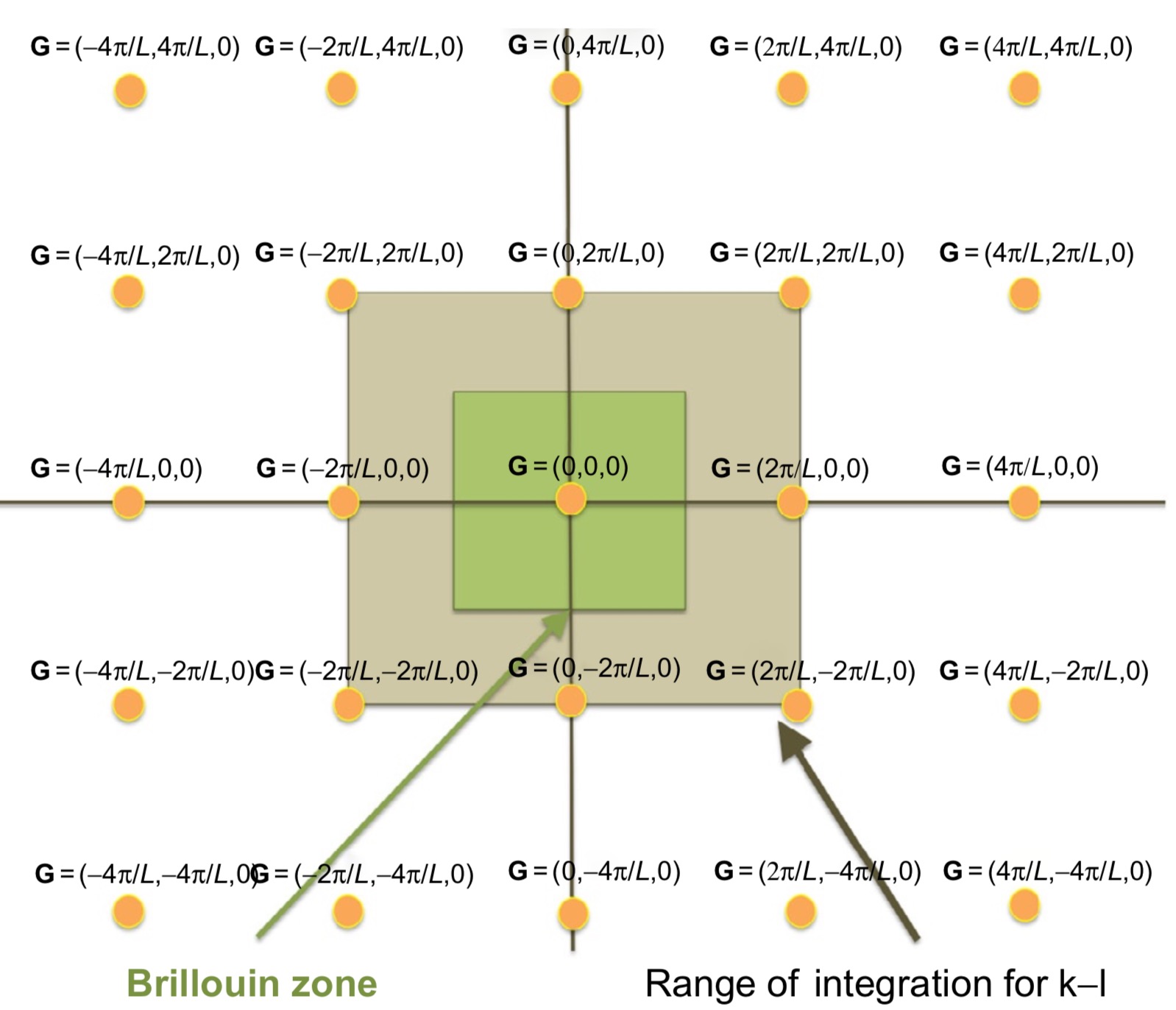
Special Points (G=0,1,2,3)
1/R Potential
1/R Potential
1/R Potential
Next Step
- Implement intergration technique in NWChem for testing with established material
- Use methods that require exact-exchange in periodic systems with multiple K-points
- Compare methods with existing gold standard
Current/Future Work
- AIMD studies on the peptide/BNNTs interface in a solvated environment
- Post-doc Position at the Army Research Laboratory
- Polymer/material with intergrated theory and experiment

Challenges
- Computation power (Hardware/Software)
- Scaling of theories (CCSD vs. DFT vs. MD)
- Inclusion of all relevant parameters (ions, solution, pH, etc.)
- Asking the right questions
Conclusion
- Laid the foundation for protein BNNT simulations
- Started to investigate functionalized structures
- Building framework for future large scale applications
- Flexibility to look at similar structures (e.g. Polymers)
Acknowledgements
- Ravindra Pandey
- Eric Bylasksa
- Gregory Odegard
- Ranjit Pati
- Max Seel
- Wil Slough
- Loredana Valenzano
- Yoke Khin Yap
- Group Members Past and Present
Questions
Publications
- Absorption and Fluorescence Properties of Eight C4 Substituted 7-Aminocoumarins
Shraddha Singh, Vaho Begoyan, Marina Tanasova, Kevin Waters, Max Seel, Ravindra Pandey
Journal of Physical Organic Chemistry
- Dynamics of Self-Assembled Cytosine Nucleobases on Graphene
Nabanita Saikia, Floyd Johnson, Kevin Waters, Ravindra Pandey
Nanotechnology
- Stability, elastic and electronic properties of a novel BN2 sheet with extended hexagons with N-N bonds
Kevin Waters, Ravindra Pandey
Journal of Physics: Condensed Matter - Hierarchical Self-Assembly of Noncanonical Guanine Nucleobases on Graphene
Nabanita Saikia, Kevin Waters, Shashi P. Karna, Ravindra Pandey
ACS Omega, vol. 2. pp. 3457, 2017 - Amino-Acid-Conjugated Gold Clusters: Interaction of Alanine and Tryptophan with Au8 and Au20
Marwa H. Abdalmoneam, Kevin Waters, Nabanita Saikia, and Ravindra Pandey
J. Phys. Chem. C, vol. 121 pp. 25585–25593, 2017 - Electronic Properties of Acetaminophen Adsorbed on 2D Clusters: A First Principles Density Functional Study
Ujjal Saikia, Nabanita Saikia, Kevin Waters, Ravindra Pandey, Munima Bora Sahariah
ChemistrySelect vol. 2 pp. 3613, 2017 - Amino Acid Analogue-Conjugated BN Nanomaterials in a Solvated Phase : First Principles Study of Topology-Dependent Interactions with a Monolayer and a (5,0) Nanotube
Kevin Waters, Ravindra Pandey, Shashi P. Karna
ACS Omega vol. 2, pp. 76−83, 2017 - Thermoelectric Properties of SnSe Nanoribbons: A Theoretical Aspect
Kriti Tyagi, Kevin Waters, Gaoxue Wang, D. Haranath, Bhasker Gahtori, Ravindra Pandey
Materials Research Express, vol. 3 pp. 35013, 2016 - A Theoretical Study of Structural and Electronic Properties of Alkaline-Earth Fluoride Clusters
Ratnesh Pandey, Kevin Waters, Sandeep Nigam, Haiying He, Subhash Pingle, Avinash Pandey, Ravindra Pandey
Computation and Theoretical Chemistry, vol. 1043, pp. 24–30, 2014